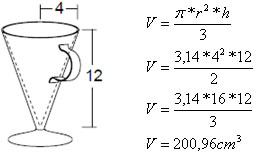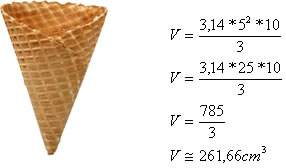Sobre o Matemática Space

O Matemática Space é uma ferramenta de ajuda sobre determinados assuntos matemáticos. Aqui serão estudados assuntos como:

→ Cilindro

→ Cone

→ Esfera

→ Números Complexos

Mas adiante estaremos colocando novos assuntos, em que todos poderão ter acesso e possivelmente a nossa ajuda.

Os Alunos envolvidos são:

* Debora Caldas

* Karoline Silva

* David Gabriel

* Fernando Portela

Esperamos ajudá-los.

Contatos:

debora_cefet@hotmail.com (Debora Caldas)

karol-jkl@hotmail.com (Karoline Silva)

Link:
http://www.baixaki.com.br/categorias/403-matematica.htm

Voltem sempre.

Números Complexos

→ Introdução

Na resolução de uma equação algébrica, um fator fundamental é o conjunto universo que representa o contexto onde poderemos encontrar as soluções. Por exemplo, se estivermos trabalhando no conjunto dos números racionais, a equação 2x+7=0, terá uma única solução dada por x=-7/2. assim, o conjunto solução será:

S = { 7/2 }

mas, se estivermos procurando por um número inteiro como resposta, o conjunto solução será o conjunto vazio, isto é:

S = Ø = { }

De forma análoga, ao tentar obter o conjunto solução para a equação x²+1=0 sobre o conjunto dos números reais, obteremos como resposta o conjunto vazio, isto é:

S = Ø = { }

o que significa que não existe um número real que elevado ao quadrado seja igual a -1, mas se seguirmos o desenvolvimento da equação pelos métodos comuns, obteremos:

x = R[-1] =

onde R[-1] é a raiz quadrada do número real -1. Isto parece não ter significado prático e foi por esta razão que este número foi chamado imaginário, mas o simples fato de substituir R[-1] pela letra i (unidade imaginária) e realizar operações como se estes números fossem polinômios, faz com que uma série de situações tanto na Matemática como na vida, tenham sentido prático de grande utilidade e isto nos leva à teoria dos números complexos.

Exemplos de tais números são apresentados na tabela.

Número complexo	Parte real	Parte imaginária
2 + 3 i	2	3
2 - 3 i	2	-3
2	2	0
3 i	0	3
-3 i	0	-3
0	0	0

Observação: O conjunto de todos os números complexos é denotado pela letra C e o conjunto dos números reais pela letra R. Como todo número real x pode ser escrito como um número complexo da forma z=x+yi, onde y=0 então assumiremos que o conjunto dos números reais está contido no conjunto dos números complexos.

→ Elementos complexos especiais

1. Igualdade de números complexos: Dados os números complexos z=a+bi e w=c+di, definimos a igualdade entre z e w, escrevendo
   
   z = w   se, e somente se,   a = c e b = d
   Para que os números complexos z=2+yi e w=c+3i sejam iguais, deveremos ter que c=2 e y=3.
   
2. Oposto de um número complexo: O oposto do número complexo z=a+bi é o número complexo denotado por -z=-(a+bi), isto é:
   
   -z = Oposto(a+bi) = (-a) + (-b)i
   O oposto de z=-2+3i é o número complexo -z=2-3i.
   
3. Conjugado de um número complexo: O número complexo conjugado de z=a+bi é o número complexo denotado por z*=a-bi, isto é:
   z* = conjugado(a+bi) = a + (-b)i
   O conjugado de z=2-3i é o número complexo z*=2+3i.
   Potências e curiosidade sobre a unidade imaginária.
   
   
   → Potências de i: 
   Ao tomar i=R[-1], temos uma sequência de valores muito simples para as potências de i:

   Potência	i2	i3	i4	i5	i6	i7	i8	i9
   Valor	-1	-i	1	i	-1	-i	1	i

   Pela tabela acima podemos observar que as potência de i cujos expoentes são múltiplos de 4, fornecem o resultado 1, logo toda potência de i pode ter o expoente decomposto em um múltiplo de 4 mais um resto que poderá ser 0, 1, 2 ou 3. Dessa forma podemos calcular rapidamente qualquer potência de i, apenas conhecendo o resto da divisão do expoente por 4.
   
   
   Curiosidade geométrica sobre i: Ao pensar um número complexo z=a+bi como um vetor z=(a,b) no plano cartesiano, a multiplicação de um número complexo z=a+bi pela unidade imaginária i, resulta em um outro número complexo w=-b+ai, que forma um ângulo reto (90 graus) com o número complexo z=a+bi dado.
   
   
   → Operações
   • Igualdade entre números complexos
   Dois números complexos são iguais se, e somente se, apresentam simultaneamente iguais a parte real e a parte imaginária. Assim, se z₁=a+bi e z₂=c+di, temos que:
   z₁=z₂<==> a=c e b=d
   • Adição de números complexos
   Para somarmos dois números complexos basta somarmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z₂=c+di, temos que:
   z₁+z₂=(a+c) + (b+d)
   • Subtração de números complexos
   Para subtrairmos dois números complexos basta subtrairmos, separadamente, as partes reais e imaginárias desses números. Assim, se z=a+bi e z₂=c+di, temos que:
   z₁-z₂=(a-c) + (b-d)

Cilindro

→ Introdução aos cilindros

O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas. Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno. 

→Aplicações práticas

Os cilindros abaixo recomendam alguma aplicação importante em sua vida? 

 

 

→ A Construção de cilindros

 

Seja P um plano e nele vamos construir um círculo de raio r. Tomemos também um segmento de reta PQ que não seja paralelo ao plano P e nem esteja contido neste plano P.

Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a PQ com uma extremidade no círculo.

Observamos que um cilindro é uma superfície no espaço R³, mas muitas vezes vale a pena considerar o cilindro com a região sólida contida dentro do cilindro. Quando nos referirmos ao cilindro como um sólido usaremos aspas, isto é, "cilindro" e quando for à superfície, simplesmente escreveremos cilindro.

A reta que contém o segmento PQ é denominada geratriz e a curva que fica no plano do "chão" é a diretriz.
 

Em função da inclinação do segmento PQ em relação ao plano do "chão", o cilindro será chamado reto ou oblíquo, respectivamente, se o segmento PQ for perpendicular ou oblíquo ao plano que contém a curva diretriz.
 

→ Objetos geométricos em um cilindro

 

Em um cilindro, podemos identificar vários elementos:

• Base
  É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.
• Eixo
  É o segmento de reta que liga os centros das bases do "cilindro".
• Altura
  A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".
• Superfície Lateral
  É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.
• Superfície Total
  É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.
• Área lateral
  É a medida da superfície lateral do cilindro.
• Área total
  É a medida da superfície total do cilindro.
• Seção meridiana de um cilindro
  É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro. 

→ Classificação dos cilindros circulares

• Cilindro circular oblíquo
  Apresenta as geratrizes oblíquas em relação aos planos das bases.
• Cilindro circular reto
  As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.
• Cilindro eqüilátero
  É um cilindro de revolução cuja seção meridiana é um quadrado.

→ Volume

Se a base é um círculo de raio r, então:

V = r² h

Cone

Ao olharmos ao nosso redor, nos deparamos com figuras geométricas de formas variadas, estudos são desenvolvidos no intuito de desvendar as propriedades de tais situações geométricas. Uma forma conhecida e muito utilizada é o cone, figura que iremos estudar.
O cone reto é uma figura de base circular gerada pela revolução de um triângulo retângulo.



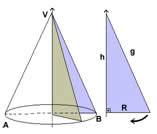Elementos de um cone

O cone é composto por uma base circular de raio (r), altura (h), vértice e lateral chamada de geratriz. No cone reto a altura é perpendicular ao centro da base de raio (r), isto é, a altura e o centro da base formam um ângulo de 90º.

Classificação e exemplos

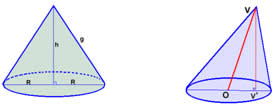
  Cone Reto                                            Cone Oblíquo 

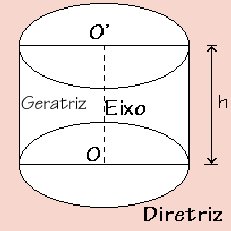
Reto

O cone é dito reto quando a sua base é uma circunferência e a reta que liga o vértice superior ao centro da circunferência da sua base é perpendicular ao plano da base. Em um cone circular reto, cuja base é um círculo, a face lateral é formada por geratrizes (g), que são linhas retas que ligam o vértice superior a pontos constituintes da circunferência do círculo. O conjunto desses pontos, ou seja, a totalidade da circunferência, tem o nome de diretriz, porque é a direção que as geratrizes tomam para criar a superfície cônica. Pode-se dizer também que o cone é gerado por um triângulo retângulo que roda sobre um eixo formado por um dos catetos, no caso de ser um cone reto. O eixo é perpendicular á base.
  
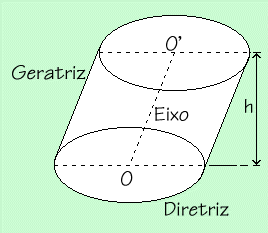
Oblíquo

Denomina-se oblíquo quando não é um cone reto, ou seja, quando o eixo é oblíquo ao plano da base.


Planificação do cone


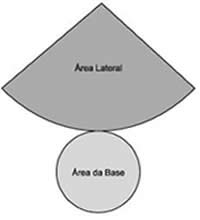Áreas pertencentes ao cone

Área da base

A área da base de um cone é a região limitada por um círculo, que pode ser calculada pela expressão: A_b = пr² (п = 3,14).

Área lateral

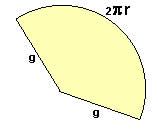
A área lateral de um cone é formada pela geratriz do cone, podemos considerá-la como o raio, veja que a planificação lateral do cone é um arco de circunferência de comprimento 2пr, pois este arco é o comprimento da base do cone. Podemos calcular a área lateral do cone utilizando a seguinte fórmula: A_L = пrg.


Área total

Calculamos a área total de um cone adicionando a área lateral e a área da base, para isso podemos utilizar a seguinte expressão:

A_t = пr (g+r)

Volume 
Para calcularmos o volume do cone multiplicamos a área da base pela medida da altura e dividimos o resultado por três. Observe: 

Exemplo 1

Um copo será fabricado no formato de um cone com as seguintes medidas: 4 cm de raio e 12 cm de altura. Qual será a capacidade do copo?

Exemplo 2

Uma casquinha de sorvete possui o formato de um cone reto com altura de 10 cm e raio da base medindo 5 cm. Determine o volume da casquinha.

Esfera

- Definição:

A esfera é um sólido limitado por uma superfície curva de revolução que tem todos os pontos igualmente distantes de um ponto interior chamado centro. A superfície esférica é resultado da revolução de uma semicircunferência em torno do diâmetro.

 

-A área da superfície de uma esfera:

Temos que a área de uma superfície esférica de raio r é igual a:

A = 4πr²

 

- Posição relativa entre plano e esfera:

- Plano secante a esfera:

O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.



- Plano tangente à esfera:

O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.




- Plano externo à esfera:
O plano e a esfera não possuem pontos em comum.

- Volume da esfera :

Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:

V = 4πr³

         3

- Fuso esférico e Cunha esférica:

 O fuso esférico pode ser entendido, como sendo uma parte superfície da esfera. E a cunha esférica uma parte do volume.  E não se tem uma fórmula concreta para se calcular ambos, então podemos calculá-los através da Regra de Três Simples.