- Definição:
A esfera é um sólido limitado por uma superfície curva de revolução que tem todos os pontos igualmente distantes de um ponto interior chamado centro. A superfície esférica é resultado da revolução de uma semicircunferência em torno do diâmetro.

-A área da superfície de uma esfera:
Temos que a área de uma superfície esférica de raio r é igual a:
A = 4πr2
- Posição relativa entre plano e esfera:
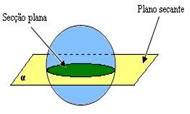
- Plano secante a esfera:
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.
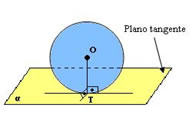
- Plano tangente à esfera:
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.
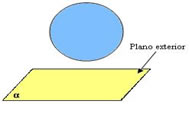
- Plano externo à esfera:
O plano e a esfera não possuem pontos em comum.
- Plano secante a esfera:
O plano intersecciona a esfera formando duas partes, se o plano corta a esfera passando pelo centro temos duas partes de tamanhos iguais.

- Plano tangente à esfera:
O plano tangencia a esfera em apenas um ponto, formando um ângulo de 90º graus com o eixo de simetria.

- Plano externo à esfera:
O plano e a esfera não possuem pontos em comum.

- Volume da esfera :
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:
Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:
V = 4πr3
3
- Fuso esférico e Cunha esférica:
- Fuso esférico e Cunha esférica:
O fuso esférico pode ser entendido, como sendo uma parte superfície da esfera. E a cunha esférica uma parte do volume. E não se tem uma fórmula concreta para se calcular ambos, então podemos calculá-los através da Regra de Três Simples.
Nenhum comentário:
Postar um comentário